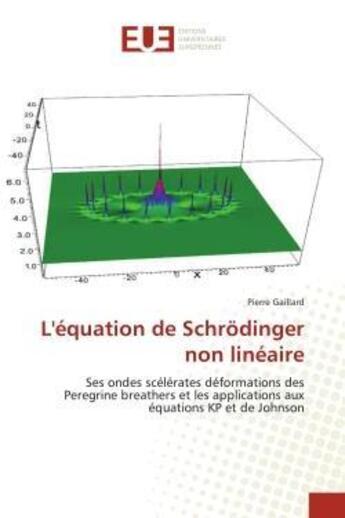
Ce texte est dévolu à l'équation de Schrodinger non linéaire focalisante (NLS). Une nouvelle approche a permis d'expliquer la formation des ondes scélérates multiples ou « rogue waves » ainsi que de décrire la génération des ondes extrêmes appelées solitons pulsés ou encore « Peregrine breathers » d'ordre N (PB). Différentes représentations des solutions de l'équation de Schrodinger non linéaire focalisante (NLS) ont été construites : en termes de wronskiens, de déterminants de Fredholm et de fonctions quasi rationnelles s'exprimant comme produits de déterminants d'ordre 2N par une exponentielle dépendant du temps. Dans ces dernières solutions, on retrouve les « Peregrine breathers » (PB) d'ordre N en choisissant tous les paramètres nuls, et pour cette raison sont appelées déformations des PB. On donne la structure des solutions quasi rationnelles de l'équation NLS à l'ordre N. On construit les déformations explicites des solutions de l'équation NLS jusqu'à l'ordre N=12 dépendant de 2N-2 paramètres et les configurations du module de ces solutions.De ces résultats, on déduit différentes représentations des solutions des équations de Kadomtsev-Petviasvili et de Johnson.
Il n'y a pas encore de discussion sur ce livre
Soyez le premier à en lancer une !
Dans ce recueil de 13 nouvelles, la jeune autrice mexicaine frappe fort mais juste
Une fiction historique glaçante et inoubliable, aux confins de l’Antarctique
Découvrez les derniers trésors littéraires de l'année !
"On n'est pas dans le futurisme, mais dans un drame bourgeois ou un thriller atmosphérique"
